[정보] KEEP!T History: 영지식 증명 이해하기
 Work4Block
Work4Block- 0
- 2,911
- 0
- 0
- 글주소
- 10-12


블록체인史영지식 증명 이해하기

안녕하세요! KEEP!T입니다.
지난 칼럼에선 익명화폐 변천사, 그리고 크립토노트 기술에 대해 다뤘습니다. 오늘은 현대 암호학의 정수 영지식 증명 기술에 대해 소개하려 합니다. 아 참, 지난 칼럼을 못보신 분들을 위해 익명화폐 변천사를 담은 계보도를 덧붙이겠습니다.
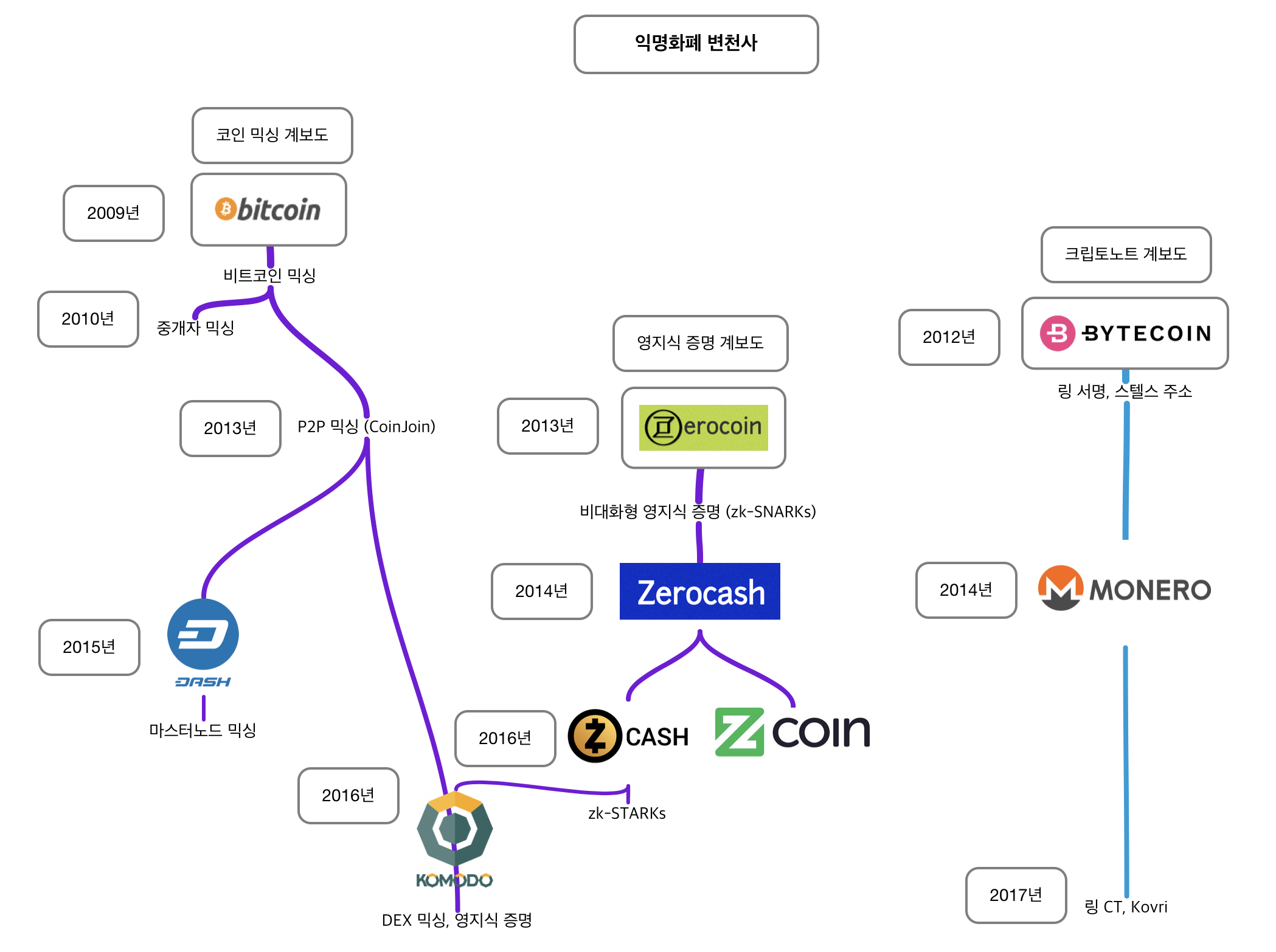
1. 영지식 증명
영지식 증명은 1985년 Shafi Goldwasser, Silvio Micali, Charles Rackoff의 논문 "The Knowledge Complexity of Interactive Proof-Systems"에서 처음 소개된 개념입니다. 최근엔 지캐시를 필두로 많은 암호화폐가 익명 거래를 지원하기 위해 영지식 증명을 도입하고 연구하고 있죠. 그럼 어떻게 해서 영지식 증명이 익명성을 보장하는지 영지식의 개념부터 차근차근 접근하도록 하겠습니다.
먼저 영지식이란 지식을 변화시키지 않는다는 것입니다. 기존의 지식에 새로운 지식을 추가하지 않는 것을 뜻합니다.
영지식 증명이란 증명자(Prover)가 알고 있는 지식을 검증자(Verifier)에게 증명할 때, 검증자의 지식을 변화시키지 않고 증명하는 방식을 뜻합니다. 검증자에게 새로운 지식을 주지 않고, 자신이 그 지식을 알고 있다는 사실만을 증명하는 겁니다.
예를 들어, 민수(증명자)가 아영이(검증자)에게 빌딩 출입문의 비밀번호를 알고 있다고 주장합니다. 민수는 자신이 그 문의 비밀번호를 알고 있다는 사실을 증명하고 싶지만, 아영이에게 직접 비밀번호를 알려주고 싶지는 않습니다. 이때 민수는 아영이에게 빌딩 반대편에 가있으라 한 다음, 빌딩 출입문을 열고 아영이가 있는 곳으로 나옵니다. 이러한 방법으로 민수는 아영이에게 비밀번호를 직접 노출하지 않고도, 자신이 그 비밀번호를 알고 있다는 사실을 증명합니다. 이는 민수가 아영이의 지식을 변화시키지 않고도 자신이 그 지식을 알고 있다는 사실을 증명한 것입니다. 처음에 아영이는 민수가 다른 사람이 출입문을 열었을 때 묻어들어간 거라 의심할 수 있습니다. 그러나 민수가 이 출입문을 10번, 100번 반복해서 나온다면, 아영이도 서서히 민수가 비밀번호를 알고 있다는 사실을 확신하게 됩니다. 이러한 반복 시행을 통해 증명자는 충분히 높은 확률로 검증자를 확신시키고, 시행이 반복될수록 영지식 증명의 신뢰도는 높아집니다.
영지식 증명이 필요한 이유는 증명자가 증명을 하기 위하여 자신이 가지고 있는 비밀 정보(secret information)를 이용할 때, 이 비밀 정보가 증명 과정(증명자와 검증자의 통신로)에서 노출되어선 안되기 때문입니다. 위 예시에서 민수가 아영이에게 직접 출입문의 비밀번호를 알려준다면, 아영이에게 보여주는 과정에서 옆에 있는 다른 사람에게 비밀 정보가 노출될 가능성도 배제할 수 없습니다.
이렇게 영지식 증명을 통하여 우리는 증명 과정에서 비밀 정보의 노출 없이, 어떤 진술에 대한 참, 거짓을 증명할 수 있게 됩니다.
영지식 증명이 되기 위해선 다음 세 가지 조건을 만족해야 합니다.
(1) 완전성(completeness)
진술이 참이라면 증명자는 검증자에게 충분히 높은 확률로 이 지식을 증명할 수 있어야 한다.
(2) 건전성(soundness)
진술이 거짓이라면 증명자는 검증자에게 아주 적은 확률로 이 지식을 증명할 수 있어야 한다.
(3) 영지식성(zero-knowledgeness)
진술이 참이면, 검증자는 이 진술이 참이란 사실 이외에는 아무것도 알 수 없어야 한다.
아래 또하나의 예시를 통해 영지식 증명의 원리를 이해해보겠습니다.
2. 두 개의 공과 색맹 친구
민수에게 색맹 친구가 있고, 두 개의 공을 가지고 있다고 가정하겠습니다. 하나는 빨간색, 하나는 초록색이지만 모양은 동일합니다. 민수의 친구에게 두 개의 공은 완전히 동일하게 보이고, 이 친구는 두 개가 구별가능한지 의심하는 상황입니다. 민수는 이 친구에게 사실 두 공이 모양은 같지만 색깔이 다르다고 증명하고 싶습니다.
증명할 수 있는 방법이 있습니다. 두 공을 친구에게 주고, 친구는 등 뒤에 공을 숨깁니다. 그리고 친구는 그 중 하나를 가져다가 보여줍니다. 그 다음 이 공을 다시 등 뒤에 숨기고, 둘 중 하나를 꺼냅니다. 처음에 보여줬던 공이 나올 확률은 50%입니다. 그리고 친구는 민수에게 묻습니다. "내가 공을 바꿨게, 안바꿨게?". 물론 민수는 처음에 봤던 공의 색깔을 알기에 당연히 맞출 수 있습니다. 필요하다면 친구가 확신할 때까지 이 과정을 반복합니다.
여기서 민수는 증명자, 색맹 친구는 검증자입니다. 충분히 많은 시행을 할 경우, 민수는 두 공에 색깔이 있다는 사실을 충분한 확률(100%에 가까운 확률)로 증명할 수 있기에, 이는 완전성을 만족시킵니다. 만약 공에 색깔이 없는 경우, 민수가 무작위로 친구가 공을 바꿨는지, 안바꿨는지를 맞출 확률은 0에 가깝습니다. 이는 건전성을 만족시킵니다. 민수는 공의 색깔이 빨간색, 초록색인 사실을 알지만, 민수의 친구는 알 수 없습니다. 민수 친구의 지식은 변하지 않았기에 이는 영지식을 만족시킵니다.
영지식 증명은 이처럼 증명자가 검증자에게 지식을 직접 노출시키지 않고도, 증명자가 지식을 알고 있다는 사실을 검증자에게 납득시킵니다. 이는 익명 거래에 있어서도 마찬가지입니다. 영지식 증명을 통해 발신자는 자신의 신원을 노출시키지 않고 수신자에게 자신이 거래 당사자란 사실을 확률적으로 증명할 수 있습니다.
익명화폐의 역사 3편에선 알리바바 동굴의 예시를 들어 영지식 증명의 원리를 설명합니다. 이 칼럼 또한 참고하시길 권해드립니다.
지금까지 코인 믹싱, 크립토노트, 영지식 증명을 통한 익명 거래의 원리를 살펴보았습니다. 그리고 이 익명화 기술의 공통점으로 확률이란 수학적 원리가 사용되고 있음을 알 수 있었습니다. 킵잇 독자분들께 익명화 기술 원리를 이해시켜드리기에 설명이 충분하진 못했으나, 익명화 기술에 대한 호기심을 키운 내용이 되었으면 합니다. 다음 시간엔 사이퍼펑크 선언문을 소개함으로써 사이퍼펑크 편을 마무리하려 합니다. 그럼 다음 칼럼으로 찾아뵙겠습니다. 감사합니다.
blockchainnomad
참고 자료
박성준, 현대암호학, 동국대학교, 2018
위키피디아, Zero-knowledge proof,
KEEP!T History
익명화폐의 역사 시리즈
익명화폐의 역사 1편 비트코인 믹싱
익명화폐의 역사 2편 대시, 모네로
익명화폐의 역사 3편 지캐시
익명화폐의 역사 4편 코모도
익명화폐의 역사 5편 익명 스마트 계약
블록체인史 시리즈
KEEP!T History: 월 스트리트 점령은 비트코인으로부터
KEEP!T History: 글로벌 경제 네트워크라는 화두
KEEP!T History: 신뢰의 문제에 도전하는 블록체인
KEEP!T History: 약자에게 프라이버시를, 강자에게 투명성을
KEEP!T History: 암호화폐의 탄생
KEEP!T Histroy: 어둠의 세력이 키운 익명화폐
KEEP!T History: 익명화폐 변천사


이 저작물은 크리에이티브 커먼즈 저작자표시-비영리-변경금지 4.0 국제 라이선스에 따라 이용할 수 있습니다.




