[자유 게시판] [과학 에세이] 양자역학, 경제학, 그리고 진화론 (1)
 Work4Block
Work4Block- 0
- 3,927
- 0
- 0
- 글주소
- 08-20

들어가며
여러분은 진화론을 믿습니까? 우리는 의무교육과정을 거치며 진화론을 정설로서 배웁니다만, 이와 별개로 진화론의 찬반에 대한 개인 간 토론을 심심치 않게 볼 수 있습니다. 하루는 제가 생명과학자이자 베스트셀러의 저자로 이름 난 최재천 교수님의 강연을 들을 기회가 있었는데, 그 자리에서도 빠지지 않았던 질문이 ‘진화론’에 대한 교수님의 견해였습니다.
한 측은 진화론을 종교적 이유로 믿지 아니하고, 한 측은 종교와 상관없이 진화론이 너무 비상식적이라서, 내용이 너무 자주 바뀌어서, 설명하지 못하는 부분이 너무 많아서 등 여러 이유로 진화론을 믿지 못하겠다고 합니다. 또 한 측은 반대측의 무지를 지적하며 과학에 대하여 설명하고 진화론을 믿어야 한다고 말합니다.
그동안 많은 사람들이 논쟁에 참전하여 왜 진화론이 옳은지를 설명해왔습니다. 미국 펜실베이니아주 법정이 진화론을 다룬 사건(법정에 선 다윈)은 이미 유명합니다. 저는 진화론을 둘러싼 논쟁들을 보던 중 문득, 진화론에 대한 논증의 내용이 아니라 이 논쟁 자체가 어딘가 부자연스럽다는 생각이 들었습니다. 이 글은 제가 느낀 그 부자연스러움에 대한 이야기입니다.
다소 엉뚱해 보이지만, 제 이야기는 양자역학을 이해하는 것으로부터 출발합니다.
양자역학
양자역학은 상대성 이론과 함께 현대물리학을 이끈 혁명적인 이론입니다. 현재 우리가 누리는 첨단 IT 기기들은 전부 양자역학 덕에 만들 수 있었습니다. 하지만 양자역학이 처음 등장하였을 당시에는 쉽게 받아들여지지 못했습니다. 공간과 시간이 왜곡된다는 황당한 주장을 내놓았던 아인슈타인마저 “신은 주사위 놀이를 하지않는다”는 명언으로 양자역학을 비판했고, 불확정성 원리를 내놓은 당사자인 하이젠베르크조차 양자역학을 부정했습니다. 양자역학이란 무엇이길래 당대의 천재 물리학자들이 반대했던 것 일까요.
양자역학은 ‘입자’의 존재를 부정합니다. 바위를 깨면 자갈이 되고 자갈을 깨면 모래가 되듯, 만물은 어떠한 기본 ‘입자’로 구성되어 있을 것이라는 매우 자연스러운 상식을 뒤엎습니다. 양자역학은 물리적 실재가 본질적으로 ‘입자’가 아닌 ‘확률파동’으로서 존재한다고 이야기합니다. ‘입자성’이라는 것은 ‘파동’이 일정 조건하에서 보여주는 한 현상에 불과합니다. ‘확률파동’이란 우리가 ‘입자’라고 믿는 것의 위치, 운동량 따위가 확률적으로만 기술될 수 있으며, 그 확률 분포가 ‘파동’의 형태를 띤다는 것을 의미합니다. 예를 들어, 전자(electron)가 아래의 ‘확률파동’을 가지고 있을 때, 전자라는 실재는 -1<x<1 에서 1/2 만큼, 1<x<3에서 1/10만큼, 3<x<5에서 1/15만큼 중첩적으로 존재합니다. 그렇다고 전자가 쪼개진 채로 존재한다는 말은 아닙니다.
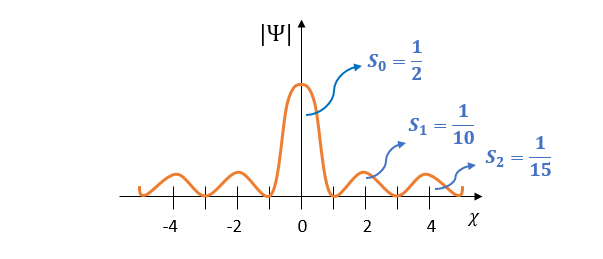
그리고 양자역학에서 ‘관측’이라는 행위는 이 ‘확률파동’을 붕괴시켜 어떠한 물리량(위치와 같은)을 특정하고, 물리적 실재에 입자성을 부여합니다. 관측 이전에는 오로지 확률로만 존재하던 것이 ‘관측’을 통해 ‘입자’가 됩니다. 여기서 양자역학은 또 한번 우리의 상식을 뒤엎습니다. 위 결과를 해석하자면, 결과가 원인에 의해 발생하지 않고, 우리가 관측한 결과에 따라 원인이 발생한 셈입니다.
물리적 실재가 확률로서 중첩적으로 존재한다거나, 결과에 의해 원인이 발생한다는 내용은 누구도 쉽게 받아 들일 수 없는 이상한 나라의 이야기처럼 들립니다. 왜 당대의 물리학자들이 양자역학에 반론을 제기했는지 이해가 가지 않습니까?
이제 한 발짝 더 나가가 양자역학에서 가장 기본 개념인, 하이젠베르크의 불확정성의 원리에 대해서도 조금 설명해보겠습니다. 불확정성의 원리란 “입자의 위치를 정확히 측정하면 운동량을 알 수 없고, 운동량을 정확히 측정하면 위치를 알 수 없게 된다”는 이론입니다. 흔히 교양서적으로 양자역학을 접한 분들은 불확정성 원리를 측량 기술의 한계 탓에 발생한다고 오해하기 쉽지만, 불확정성의 원리는 수학적 논리의 귀결입니다. 모두 알다시피, 모든 파동 함수는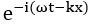 를 기저(basis)로 하여 생성(span)된 함수공간에서 기술될 수 있고, 양자역학의 가정에 따라 기저를
를 기저(basis)로 하여 생성(span)된 함수공간에서 기술될 수 있고, 양자역학의 가정에 따라 기저를 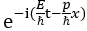 로 나타낼 수 있습니다. 이때 운동량 p와 위치 x는 서로 상보적 관측가능값(commuting observable)이라는 것을 알 수 있습니다. 쉽게 말해 x 도메인 상의 파동함수는 p 도메인 상의 파동함수로 푸리에 변환(Fourier transform)될 수 있는 관계이므로, 특정 x값에 확률이 집중될수록 p의 확률분포는 더 평평하게 퍼진다는 말입니다. 아래 그림은 이해를 돕기 위해 극단적인 상황을 가정하여, x 도메인 상에 디렉 델타(Dirac Delta)로 분포를 갖는 확률 함수가 p 도메인에서 어떻게 그려지는지를 나타냅니다.
로 나타낼 수 있습니다. 이때 운동량 p와 위치 x는 서로 상보적 관측가능값(commuting observable)이라는 것을 알 수 있습니다. 쉽게 말해 x 도메인 상의 파동함수는 p 도메인 상의 파동함수로 푸리에 변환(Fourier transform)될 수 있는 관계이므로, 특정 x값에 확률이 집중될수록 p의 확률분포는 더 평평하게 퍼진다는 말입니다. 아래 그림은 이해를 돕기 위해 극단적인 상황을 가정하여, x 도메인 상에 디렉 델타(Dirac Delta)로 분포를 갖는 확률 함수가 p 도메인에서 어떻게 그려지는지를 나타냅니다.
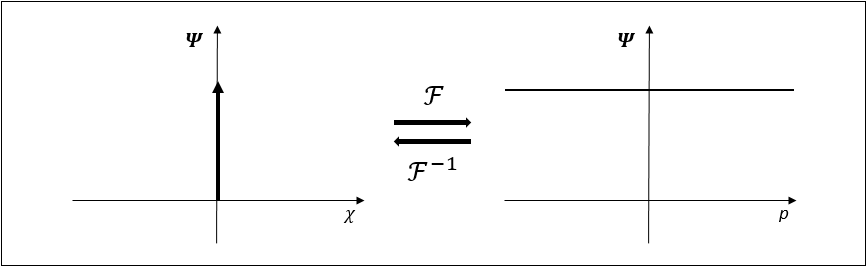
참 쉽죠?

난데없이 알 수 없는 용어와 그래프, 수식이 등장해서 놀라셨나요? 하지만 양자역학은 수학없이 제대로 이해하기 무척 어려운 학문입니다. 그러면서도 동시에 차라리 수학을 동원해 양자역학을 ‘하는 것’이, 양자역학을 ‘이해하는 것’보다 쉬운 학문이 양자역학입니다.
양자역학은 너무나도 ‘비상식적’ 입니다. ‘상식’은 일반적 견문과 함께 이해력, 판단력, 사리 분별 따위를 말하지만, 양자역학은 어느 누구도 경험해 본 적이 없는 매우 작은 공간에서 일어나는 일을 설명합니다. 당연히 상식적일리가 없습니다. 심지어, 양자역학은 아직도 그 해석에 대하여 의견이 분분하게 나뉩니다. 현재는 ‘코펜하겐 해석’을 표준으로 삼고 저도 그 해석대로 설명을 드렸지만, 누구도 이를 확신하지 못합니다. 20세기의 천재 물리학자 리처드 파인만조차 “나는 누구도 양자역학을 이해하지 못했다고 생각한다”는 말을 하였으니까요.
즉, 글을 보고 있는 당신이 아래와 같은 반응이라면 당신은 매우 상식적인 분입니다.

다만, 여러분이 양자역학을 이해하는 걸 포기한 지금, 한가지 질문이 있습니다. 여러분은 양자역학을 믿습니까?
(쓰다보니 글이 길어 둘로 나눕니다)
양자역학, 경제학, 그리고 진화론 (2)로 이어집니다.




